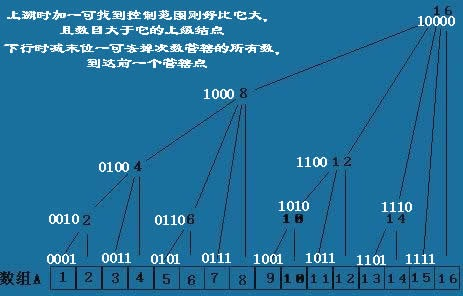
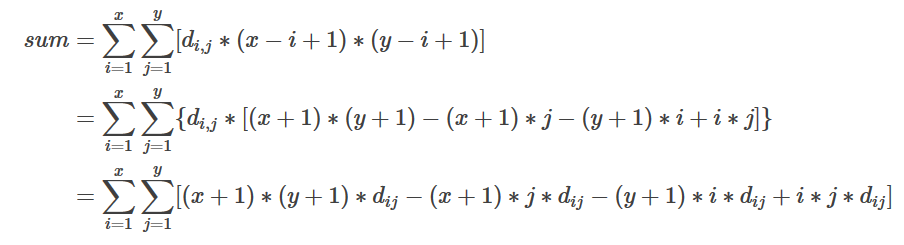一条无向边需要四倍(也可以两倍)空间,有向边需要两倍空间 若有总流量上限,可以添加边0~1和n~n+1,cap为上限,cost为0,s=0,t=n+1 若求特定流量下的最小费用,需修改mincost_maxflow,并判断是否能达到该流量
spfa版 时间复杂度\(O(Fnm)\)
(一看就不怎么靠谱) 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
using namespace std;
int head[5005],vet[100005],nxt[100005],cap[100005],cost[100005],num;
long long dist[5005];
int prev[5005];
bool inque[5005];
int n,m,s,t;
int flow,Cost;
void addedge(int x,int y,int ca,int co) {
num++;vet[num]=y;cap[num]=ca;cost[num]=co;nxt[num]=head[x];head[x]=num;
num++;vet[num]=x;cap[num]=0;cost[num]=-co;nxt[num]=head[y];head[y]=num;
}
bool spfa(int s,int t) {
queue<int> que;
for (int i=1;i<=n;i++) dist[i]=1e12,inque[i]=false,prev[i]=-1;
que.push(s);dist[s]=0;inque[s]=true;
while (!que.empty()) {
int u=que.front();que.pop();
inque[u]=false;
for (int e=head[u];e!=-1;e=nxt[e]) {
int v=vet[e];
if(cap[e]>0 && dist[v]>dist[u]+cost[e]) {
dist[v]=dist[u]+cost[e];
prev[v]=e;
if (!inque[v]) {
inque[v]=true;
que.push(v);
}
}
}
}
if (dist[t]==1e12) return false;
else return true;
}
void mincost_maxflow(int s,int t) {
while (spfa(s,t)) {
int ff=1e9;
for (int i=t;i!=s;i=vet[prev[i]^1]) ff=min(ff,cap[prev[i]]);
Cost+=ff*dist[t];
flow+=ff;
for (int i=t;i!=s;i=vet[prev[i]^1]) {
cap[prev[i]]-=ff;
cap[prev[i]^1]+=ff;
}
}
}
int main() {
scanf("%d%d%d%d",&n,&m,&s,&t);
memset(head,-1,sizeof(head));num=-1;
for (int i=1;i<=m;i++) {
int x,y,w,c;
scanf("%d%d%d%d",&x,&y,&w,&c);
addedge(x,y,w,c);
}
mincost_maxflow(s,t);
printf("%d %d\n",flow,Cost);
return 0;
}
dijkstra版 算法原理
如果一开始就有负权边,需要先跑一遍spfa
1.不带堆优化,时间复杂度\(O(Fn^2)\)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
using namespace std;
int head[5005],vet[100005],nxt[100005],cap[100005],cost[100005],num;
long long dist[5005],h[5005];
int prev[5005];
bool used[5005];
int n,m,s,t;
int flow,Cost;
void addedge(int x,int y,int ca,int co) {
num++;vet[num]=y;cap[num]=ca;cost[num]=co;nxt[num]=head[x];head[x]=num;
num++;vet[num]=x;cap[num]=0;cost[num]=-co;nxt[num]=head[y];head[y]=num;
}
bool dijkstra(int s,int t) {
for (int i=1;i<=n;i++) dist[i]=1e12,used[i]=false,prev[i]=-1;
dist[s]=0;
for (int i=1;i<=n;i++) {
int mindist=1e12,p=0;
for (int j=1;j<=n;j++)
if (!used[j] && mindist>dist[j]) {
mindist=dist[j];
p=j;
}
used[p]=true;
for (int e=head[p];e!=-1;e=nxt[e]) {
int v=vet[e];
if (cap[e]>0 && dist[v]>dist[p]+cost[e]+h[p]-h[v]) {
dist[v]=dist[p]+cost[e]+h[p]-h[v];
prev[v]=e;
}
}
}
if (dist[t]==1e12) return false;
else return true;
}
void mincost_maxflow(int s,int t) {
memset(h,0,sizeof(h));
while (dijkstra(s,t)) {
for (int i=1;i<=n;i++) h[i]+=dist[i];
int ff=1e9;
for (int i=t;i!=s;i=vet[prev[i]^1]) ff=min(ff,cap[prev[i]]);
Cost+=ff*h[t];
flow+=ff;
for (int i=t;i!=s;i=vet[prev[i]^1]) {
cap[prev[i]]-=ff;
cap[prev[i]^1]+=ff;
}
}
}
int main() {
scanf("%d%d%d%d",&n,&m,&s,&t);
memset(head,-1,sizeof(head));num=-1;
for (int i=1;i<=m;i++) {
int x,y,w,c;
scanf("%d%d%d%d",&x,&y,&w,&c);
addedge(x,y,w,c);
}
mincost_maxflow(s,t);
printf("%d %d\n",flow,Cost);
return 0;
}
2.使用堆优化,时间复杂度\(O(Fnlogm)\) 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
using namespace std;
typedef long long LL;
struct node {
LL dis,po;
bool operator<(const node &res) const {
return dis>res.dis;
}
};
int head[5005],vet[100005],nxt[100005],cap[100005],cost[100005],num;
LL dist[5005],h[5005];
int prev[5005];
bool used[5005];
int n,m,s,t;
int flow,Cost;
void addedge(int x,int y,int ca,int co) {
num++;vet[num]=y;cap[num]=ca;cost[num]=co;nxt[num]=head[x];head[x]=num;
num++;vet[num]=x;cap[num]=0;cost[num]=-co;nxt[num]=head[y];head[y]=num;
}
bool dijkstra(int s,int t) {
priority_queue<node> que;
for (int i=1;i<=n;i++) dist[i]=1e12,used[i]=false,prev[i]=-1;
que.push((node){0,s});dist[s]=0;
while (!que.empty()) {
int u=que.top().po;que.pop();
if (used[u]) continue;
used[u]=true;
for (int e=head[u];e!=-1;e=nxt[e]) {
int v=vet[e];
if (cap[e]>0 && dist[v]>dist[u]+cost[e]+h[u]-h[v]) {
dist[v]=dist[u]+cost[e]+h[u]-h[v];
prev[v]=e;
que.push((node){dist[v],v});
}
}
}
if (dist[t]==1e12) return false;
else return true;
}
void mincost_maxflow(int s,int t) {
memset(h,0,sizeof(h));
while (dijkstra(s,t)) {
for (int i=1;i<=n;i++) h[i]+=dist[i];
int ff=1e9;
for (int i=t;i!=s;i=vet[prev[i]^1]) ff=min(ff,cap[prev[i]]);
Cost+=ff*h[t];
flow+=ff;
for (int i=t;i!=s;i=vet[prev[i]^1]) {
cap[prev[i]]-=ff;
cap[prev[i]^1]+=ff;
}
}
}
int main() {
scanf("%d%d%d%d",&n,&m,&s,&t);
memset(head,-1,sizeof(head));num=-1;
for (int i=1;i<=m;i++) {
int x,y,w,c;
scanf("%d%d%d%d",&x,&y,&w,&c);
addedge(x,y,w,c);
}
mincost_maxflow(s,t);
printf("%d %d\n",flow,Cost);
return 0;
}