GGAutomaton's Blog
0%

发表于 分类于 ，

匈牙利算法
时间复杂度：\(O(nm)\) 

1
2
3
4
5
6
7
8
9
10
11
12
bool dfs(int x) {
	for (int e=head[x];e;e=nxt[e]) {
		int v=vet[e];
		if (vis[v]) continue;
		vis[v]=1;
		if (match[v]==-1 || dfs(match[v])) {
			match[v]=x;
			return true;
		}
	}
	return false;
}
1
2
3
4
5
6
7
int ans=0;
memset(match,-1,sizeof(match));
for (int i=1;i<=n;i++) {
	memset(vis,0,sizeof(vis));
	if (dfs(i)) ans++;
}

发表于 分类于 ， 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
struct mat {
	int r,c;
	LL data[105][105];
	mat() {r=c=0;memset(data,0,sizeof(data));}
	inline void init(int x,int y) {r=x,c=y;memset(data,0,sizeof(data));}
};
mat operator *(const mat &a,const mat &b) {
	mat tmp;tmp.init(a.r,b.c);
    if (a.c!=b.r) {tmp.r=tmp.c=0;return tmp;}
	for (int i=0;i<=a.r;i++) {
		for (int j=0;j<=b.c;j++) {
			for (int k=0;k<=a.c;k++)
				tmp.data[i][j]=(tmp.data[i][j]+a.data[i][k]*b.data[k][j])%P;
		}
	}
	return tmp;
}
inline mat fastpow(int x) {
	mat tmp;tmp.init(m+1,m+1);
	for (int i=0;i<=m+1;i++) tmp.data[i][i]=1;
	mat base=s;
	while (x>0) {
		if (x&1) tmp=tmp*base;
		base=base*base;
		x>>=1;
	}
	return tmp;
}

发表于 分类于 ，

day -2 & -1

别人停课两周，我停课两天。

day 0

两三年没坐飞机了吧。
机长的操作真是稳，落地刹车急转弯，一位老兄的手机都滑掉了。

帝都超级热啊。挥汗如雨。
被拦在 THU 门口，保安尽职尽责。

晚上背模板，十一点半睡觉。

day 1

爆炸的一天从此开始。

上午

作为一个酱油选手（dalao们可以右上角退出），遇到了很多锅。
迟到半小时，发现是 Windows 的电脑。（注：正式选手是 Ubuntu）
i7-4790，16G，R7 240 居然奇卡无比。

第一题 求区间 LIS，\(n≤10^5,q≤10^7,a_i≤10^3\) ，强制在线，1G，10s。
第一次见到这么毒瘤的范围。想到平时的单调队列二分求法，只有30pt。
直觉觉得和 \(a_i\) 有关。
猜想可持久化单调队列，搞不出。
猜想两个LIS合并，发现合并一次O(1000)，爆炸。
猜想O(1)回答询问，没思路。
至此，比赛已经过了两个半小时。 是的，我太菜了。

退回到最基本的 dp，考虑如何在 LIS 的末尾接上一个数，条件是 \(k<j\) 且 \(a[k]<a[j]\) 。
设 dp[i][j] 表示 满足 LIS 长度为 i，最后一位是 a[j] 的串，最靠右（解决 LIS 不唯一的问题）的起始位置。
外层循环 j，内层循环 i，转移需要知道 LIS 长度为 i-1，最后一位满足 \(k<j\) 且 \(a[k]<a[j]\) 的 dp[i-1][k] 的最大值。显然 LIS 长度≤1000。考虑给每个 LIS 长度 i 建一个树状数组，下标是 a[j]，值是 dp[i][j] 。不断取 max，转移就显然了。

1
2
3
dp[i][j]=query(i-1,a[j]-1);
update(i,a[j],dp[i][j]);
dp[i][j]=max(dp[i][j],dp[i][j-1]);
询问的时候二分，找到 dp[x][ri]≥li 的最大的x即可。
吐槽一下强制在线的方式，迭代值爆int。

第二题 字符串题。没时间了，暴力分也不多，跳过。

第三题 好评！人工智障！
有史以来做过最有趣的提交答案题。
你需要猜想什么输入运行 ./ai 后能够输出样例。10个点的数据，每个点有4种难度，挑一个就行。
下发的文件是 Ubuntu 的，Windows 又出锅了。等着管理员把 win 版本的 ai.exe发过来。

然后遇到了换行符问题。ai.exe 显示的行数不对。

凉凉。本机答案正确，上传发生SPJ ERROR。
由于时间不够，后面的数据还没做来得及下去。本来多个二三十分没问题。
rating估计前70吧。爆炸。

下午

subway好吃！

听吴建平教授、吴文虎教授、王逸松同学讲话。
王逸松同学：“……，不是体现在你的代码能跑多快。”

然后逛清华园。
清华真是大。但它的美不是体现在气势宏大，而是在细节处宛如苏州园林的美。
水木清华，荷塘月色。

day 2

上午

今天没有遇到锅。

第三题
拿到题先看提答。
题意：给出若干个 \(?×?\) 的小方块，将它们拼成一个大方块。小方块可以旋转，方块之间可以有空隙。利用率越高得分越高。同时要求拼出的大方块有一边的边长满足 \(L≤x≤R\) ，否则另外扣分。输出大方块剪成小方块的方案。

第一个点的方案提示很明显，就是手玩输出方案比较麻烦。
第三个点 L=R=2 ，同时所有小方块有一边边长是 1。做背包即可。（有一个 1×2的方块要竖着放）
别的一眼看不出。通解好难打，暂时跳过。

第一题
题面和洛谷5月月赛太极剑类似。所有的连边只在奇数点之间，偶数点之间可以发出能量。但是切断一条连边需要一定的能量，求切断所有连边所需的最小总能量，并输出一种方案。

出题人本来想令所有连边切断能量都等于 1，那就是月赛原题了 QwQ。出题人本来还不知道月赛这回事。
当时在做月赛的时候就在想，可以用差分约束，但是数据范围大，过不了。题解给了一种线性方法，但是没看懂。可惜对考试题不适用。
考试题的范围 \(n≤2000\) 是可以用差分约束的。果断开始建图，交上去 WA 了好几次，后来发现建边错了。

第二题 题意：一个点有 Ri 只红色史莱姆，Gi 只绿色史莱姆。所有史莱姆互不相同。给出一棵以 1 为根的树。每次从 1 出发，不能走回头路，到叶子时停止。在每个点收集且只能收集 1 只史莱姆。求分别收集到 0~n 只史莱姆的方案数。不同的史莱姆算不同的方案。

一看就是 FFT 之类的东西，是个卷积。可我就是不会。背板子有什么用？又不会用。
打完 dp 滚粗。

下午

讲题。

d1t1 dp。34人AC
d1t2 AC自动机上乱搞。
d1t3 平均得分30+。数据点记不清了。有求定积分，定位，行列式……第九个点好评，但是女主出锅了。出题者：如何评价 THUSC 2018？ - 赵金昊的回答 - 知乎

d2t1 差分约束系统。震惊！仅 10 人有分，1 人AC。个人觉得这题还算简单。
d2t2 长链剖分，分治 NTT。震惊！这是全场平均分最高的题。
d2t3 模拟退火跑数小时。

day 3

由于是酱油选手，也就没有什么面试之类的东西了。
下午听讲座，学长讲清华的学生活动。

最后，恭喜 rank1 的司机获得无条件一本资格。这次只签了十来个一本。

发表于 分类于 ，

LOJ2289
看到加边减边想到LCT
猜到要合并函数，然后看到“小R教你学数学”
果断泰勒展开

以下所有结果均令\(x_0=0\)
\[\sin(ax+b) = \sin(b) + \frac{a\cos(b)}{1!}x - \frac{a^2\sin(b)}{2!}x^2 - \frac{a^3\cos(b)}{3!}x^3 +\frac{a^4\sin(b)}{4!}x^4 + ...\]

\[e^{ax+b} = e^b + \frac{ae^b}{1!}x + \frac{a^2e^b}{2!}x^2 + \frac{a^3e^b}{3!}x^3 + \frac{a^4e^b}{4!}x^4 + ...\]

\[ax+b = b + \frac{a}{1!}x\]

计算误差发现需要展开17项，实测11项可过

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
#include<iostream>
#include<cstdio>
#include<cmath>
#include<algorithm>
using namespace std;
double val[200005][17],s[200005][17];
long long jc[17];
int ch[200005][2],fa[200005];
bool reversed[200005];
int sta[200005],top;
int n,m;
inline void reverse(int x) {
    swap(ch[x][0],ch[x][1]);
    reversed[x]^=1;
}
inline void pushdown(int x) {
    if (reversed[x]) {
        if (ch[x][0]) reverse(ch[x][0]);
        if (ch[x][1]) reverse(ch[x][1]);
        reversed[x]=0;
    }
}
inline void pushup(int x) {
	for (int i=0;i<17;i++) {
		s[x][i]=s[ch[x][0]][i]+s[ch[x][1]][i]+val[x][i];
	}
}
inline bool notroot(int x) {
    return (ch[fa[x]][0]==x)||(ch[fa[x]][1]==x);
}
inline void rotate(int x) {
    int fa1=fa[x],fa2=fa[fa1],side=(ch[fa1][1]==x),c=ch[x][side^1];
    fa[x]=fa2;if (notroot(fa1)) ch[fa2][ch[fa2][1]==fa1]=x;
    ch[fa1][side]=c;if (c) fa[c]=fa1;
    fa[fa1]=x;ch[x][side^1]=fa1;
    pushup(fa1);pushup(x);
}
inline void splay(int x) {
    int u=x,top=0;
    while (notroot(u)) sta[++top]=u,u=fa[u];
    sta[++top]=u;
    while (top) pushdown(sta[top--]);
    while (notroot(x)) {
        int fa1=fa[x],fa2=fa[fa1];
        if (notroot(fa1)) {
            if ((ch[fa2][0]==fa1)^(ch[fa1][0]==x)) rotate(x);
            else rotate(fa1);
        }
        rotate(x);
    }
}
inline void access(int x) {
    int u=0;
    while (x!=0) {
        splay(x);
        ch[x][1]=u;
        pushup(x);
        u=x;
        x=fa[x];
    }
}
inline void makeroot(int x) {
    access(x);splay(x);
    reverse(x);
}
inline int findroot(int x) {
    access(x);splay(x);
    while (ch[x][0]) pushdown(x),x=ch[x][0];
    splay(x);
    return x;
}
inline bool split(int x,int y) {
    makeroot(x);
    if (findroot(y)!=x) return false;
    access(y);splay(y);
    return true;
}
inline void link(int x,int y) {
    makeroot(x);
    if (findroot(y)!=x) fa[x]=y;
}
inline void cut(int x,int y) {
    makeroot(x);
    if (findroot(y)==x && fa[y]==x && ch[x][1]==y) {
        fa[y]=ch[x][1]=0;
        pushup(x);
    }
}
inline void modify(int i,int op,double a,double b) {
	if (op==1) {
		double tmp=1;
    	for (int j=0;j<17;j++) {
    		if (j%4==0) val[i][j]=tmp*sin(b);
    		else if (j%4==1) val[i][j]=tmp*cos(b);
    		else if (j%4==2) val[i][j]=-tmp*sin(b);
    		else val[i][j]=-tmp*cos(b);
    		tmp*=a;
		}
	}
	else if (op==2) {
   		double tmp=1,tmp2=exp(b);
   		for (int j=0;j<17;j++) {
   			val[i][j]=tmp*tmp2;
   			tmp*=a;
		}
	}
	else {
   		val[i][0]=b;val[i][1]=a;
   		for (int j=2;j<17;j++) val[i][j]=0;
	}
}
int main() {
    scanf("%d%d",&n,&m);
	char str[15];scanf("%s",str);
    jc[0]=1;
    for (int i=1;i<17;i++) jc[i]=jc[i-1]*i;
    for (int i=1;i<=n;i++) {
    	int op;double a,b;
    	scanf("%d%lf%lf",&op,&a,&b);
    	modify(i,op,a,b);
	}
    int x,y;
    while (m--) {
    	scanf("%s%d%d",str,&x,&y);
    	x++;y++;
        if (str[0]=='t') {
        	double c;
        	scanf("%lf",&c);
            if (!split(x,y)) {
            	puts("unreachable");
            	continue;
			}
            double ans=0,tmp=1;
            for (int i=0;i<17;i++) {
            	ans+=s[y][i]*tmp/jc[i];
            	tmp*=c;
			}
            printf("%.8e\n",ans);
        }
        else if (str[0]=='a') link(x,y);
        else if (str[0]=='d') cut(x,y);
        else if (str[0]=='m') {
        	double a,b;y--;
        	scanf("%lf%lf",&a,&b);
			splay(x);
			modify(x,y,a,b);
			pushup(x);
		}
    }
    return 0;
}

发表于 分类于 ，

怎样更好地理解并记忆泰勒展开式？ - 陈二喜的回答 - 知乎
终于知道那两个余项是怎么推出来的了。

这里放几个结论，方便复习。
泰勒公式：
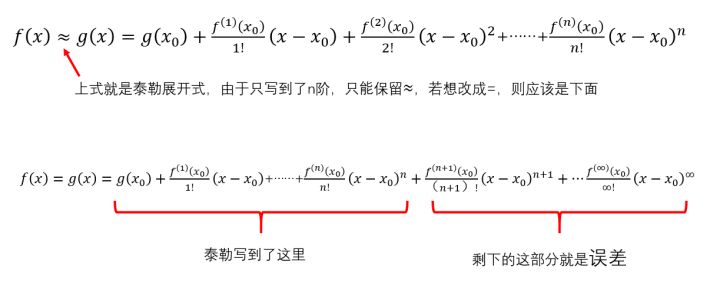Peano余项：
Lagrange余项：

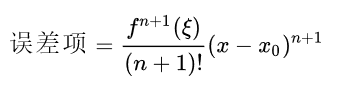
oi中用的比较多的还是麦克劳林展开：
计算一下误差的最大值，再决定展开几项。

泰勒展开的更多注意事项：泰勒公式（泰勒展开式，泰勒中值定理）使用基本技巧

发表于 分类于 ，

常见函数的狄利克雷卷积：

关于gcd(i,j)
\[gcd(i,j) = \sum_{d|gcd(i,j)} \varphi(d)\]

如果在一些奇怪的位置，可设其为d，进行枚举。 也可以设其为p(x)，进行反演。

关于gcd(i,j)==1
等价于\[\sum_{d|gcd(i,j)} \mu(d)\]

关于同时枚举p和d
可以枚举它们的积 \(T\) ，设 \(d | T\) ，这样它们就是 \(d\) 和 \(\frac{T}{d}\) 了

发表于 分类于 ，

此程序求最小原根 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
#include<iostream>
#include<cstdio>
#include<cmath>
using namespace std;
typedef long long LL;
int P,yg;
int ys[100005],nn;
LL getphi(int n) {
	LL phi=n;
	for (LL i=2;i*i<=n;i++) {
		if (n%i==0) {
			phi=phi/i*(i-1);
			while (n%i==0) n/=i;
		}
	}
	if (n>1) phi=phi/n*(n-1);
	return phi;
}
void getyueshu(int n) {
	for (int i=1;i*i<=n;i++) 
		if (n%i==0) ys[++nn]=i;
	if (ys[nn]*ys[nn]==n) nn--;
	for (int i=nn;i>0;i--) ys[++nn]=n/ys[i];
}
LL fast_pow(LL B,LL x) {
    LL tmp=1;
    while (x>0) {
        if (x&1) tmp=tmp*B%P;
        B=B*B%P;
        x>>=1;
    }
    return tmp;
}
int main() {
	cin>>P;
	int phi=getphi(P);//若是质数直接phi=P-1 
	getyueshu(phi);
	for (int i=1;i<P;i++) {//1是2的原根 
		if (fast_pow(i,phi)!=1) continue;
		bool flag=true;
		for (int j=1;j<nn;j++) {
			if (fast_pow(i,ys[j])==1) {
				flag=false;
				break;
			}
		}
		if (flag) {printf("%d",i);return 0;}
	}
	puts("-1");
	return 0;
}

发表于 分类于 ，

1.欧拉函数性质和求法：https://blog.csdn.net/yxuanwkeith/article/details/52387873
两种方法： 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
#include<iostream>
#include<cstdio>
#include<cmath>
using namespace std;
typedef long long LL;
int phi[1000005],prime[1000005];
bool f[100005];
LL getphi(LL n) {
	LL phi=n;
	for (LL i=2;i*i<=n;i++) {
		if (n%i==0) {
			phi=phi/i*(i-1);
			while (n%i==0) n/=i;
		}
	}
	if (n>1) phi=phi/n*(n-1);
	return phi;
}
int main() {
	int n;
	cin>>n;
	
	cout<<getphi(n)<<endl;
	
	phi[1]=1;
	for (LL i=2;i<=n;i++) {
		if (!f[i]) {
			phi[i]=i-1;
			prime[++prime[0]]=i;
		}
		for (int j=1;j<=prime[0];j++) {
			if (i*prime[j]>n) break;
			f[i*prime[j]]=1;
			if (i%prime[j]==0) {
				phi[i*prime[j]]=phi[i]*prime[j];
				break;
			}
			else phi[i*prime[j]]=phi[i]*(prime[j]-1);
		}
	}
	
	for (int i=1;i<=n;i++) cout<<phi[i]<<' ';cout<<endl;
	return 0;
}

2.莫比乌斯函数 https://www.cnblogs.com/Milkor/p/4464515.html
两种方法： 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
#include<iostream>
#include<cstdio>
#include<cmath>
using namespace std;
typedef long long LL;
int miu[1000005],prime[1000005];
bool f[100005];
LL getmiu(int n) {
	int s=0;
	for (LL i=2;i*i<=n;i++) {
		if (n%i==0) {
			s++;
			int cnt=0;
			while (n%i==0) n/=i,cnt++;
			if (cnt>=2) return 0;
		}
	}
	if (n>1) s++;
	if (s&1) return 1;
	else return 0;
}
int main() {
	int n;
	cin>>n;
	
	cout<<getmiu(n)<<endl;
	
	miu[1]=1;
	for (LL i=2;i<=n;i++) {
		if (!f[i]) {
			miu[i]=-1;
			prime[++prime[0]]=i;
		}
		for (int j=1;j<=prime[0];j++) {
			if (i*prime[j]>n) break;
			f[i*prime[j]]=1;
			if (i%prime[j]==0) {
				miu[i*prime[j]]=0;
				break;
			}
			else miu[i*prime[j]]=-miu[i];
		}
	}
	
	for (int i=1;i<=n;i++) cout<<miu[i]<<' ';cout<<endl;
	return 0;
}

发表于 分类于 ，

此题可以用spfa，也可以用LCT。
可spfa跑得比LCT快……

学习了一下怎么把边权变成点权：
新建一个点表示边，这个点的点权就是边权值
原来的点的权值为0（根据题目需要可以为其他值）
添加一条边时，连接两端的点
删除一条边时，需要找到这条边对应的点编号，两端删除 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
#include<iostream>
#include<cstdio>
#include<algorithm>
using namespace std;
struct node {
	int u,v,a,b;
	bool operator<(const node &res) const{
		return a<res.a;
	}
} edge[100005];
int FA[50005];
int val[150005],mx[150005],po[150005];
int ch[150005][2],fa[150005];
bool reversed[150005];
int sta[150005],top;
int n,m,ans=1e9;
inline int read() {
	char ch=0;int sum=0;
	while (ch>'9'||ch<'0') ch=getchar();
	while (ch>='0'&&ch<='9') sum=sum*10+ch-'0',ch=getchar();
	return sum;
}
int find(int x) {
	if (FA[x]!=x) FA[x]=find(FA[x]);
	return FA[x];
}
inline void Union(int x,int y) {
	FA[find(x)]=find(y);
}
inline void reverse(int x) {
	swap(ch[x][0],ch[x][1]);
	reversed[x]^=1;
}
inline void pushdown(int x) {
	if (reversed[x]) {
		if (ch[x][0]) reverse(ch[x][0]);
		if (ch[x][1]) reverse(ch[x][1]);
		reversed[x]=0;
	}
}
inline void pushup(int x) {
	int pp=x,tmp=val[x];
	if (mx[ch[x][1]]>tmp) pp=po[ch[x][1]],tmp=mx[ch[x][1]];
	if (mx[ch[x][0]]>tmp) pp=po[ch[x][0]],tmp=mx[ch[x][0]];
	po[x]=pp;mx[x]=tmp;
}
inline bool notroot(int x) {
	return (ch[fa[x]][0]==x)||(ch[fa[x]][1]==x);
}
inline void rotate(int x) {
	int fa1=fa[x],fa2=fa[fa1],side=(ch[fa1][1]==x),c=ch[x][side^1];
	fa[x]=fa2;if (notroot(fa1)) ch[fa2][ch[fa2][1]==fa1]=x;
	ch[fa1][side]=c;if (c) fa[c]=fa1;
	fa[fa1]=x;ch[x][side^1]=fa1;
	pushup(fa1);pushup(x);
}
inline void splay(int x) {
	int u=x,top=0;
	while (notroot(u)) sta[++top]=u,u=fa[u];
	sta[++top]=u;
	while (top) pushdown(sta[top--]);
	while (notroot(x)) {
		int fa1=fa[x],fa2=fa[fa1];
		if (notroot(fa1)) {
			if ((ch[fa2][0]==fa1)^(ch[fa1][0]==x)) rotate(x);
            else rotate(fa1);
		}
		rotate(x);
	}
}
inline void access(int x) {
	int u=0;
	while (x!=0) {
		splay(x);
		ch[x][1]=u;
		pushup(x);
		u=x;
		x=fa[x];
	}
}
inline void makeroot(int x) {
	access(x);splay(x);
	reverse(x);
}
inline int findroot(int x) {
	access(x);splay(x);
	while (ch[x][0]) pushdown(x),x=ch[x][0];
	splay(x);
	return x;
}
inline void split(int x,int y) {
	makeroot(x);
	access(y);splay(y);
}
inline void link(int x,int y) {
	makeroot(x);
	if (findroot(y)!=x) fa[x]=y;
}
inline void cut(int x,int y) {
	makeroot(x);
	if (findroot(y)==x && fa[y]==x && ch[x][1]==y) {
		fa[y]=ch[x][1]=0;
		pushup(x);
	}
}
inline void addedge(int i) {
	int u=edge[i].u,v=edge[i].v;
	if (find(u)!=find(v)) {
		Union(u,v);
		val[i+n]=mx[i+n]=edge[i].b;
		po[i+n]=i+n;
		link(u,i+n);
		link(v,i+n);
	}
	else {
		split(u,v);
		if (edge[i].b<mx[v]) {
			int w=po[v];
			cut(w,edge[w-n].u);
			cut(w,edge[w-n].v);
			val[i+n]=mx[i+n]=edge[i].b;
			po[i+n]=i+n;
			link(u,i+n);
			link(v,i+n);
		}
	}
}
int main() {
	n=read(),m=read();
	for (int i=1;i<=m;i++) {
		edge[i].u=read();edge[i].v=read();
		edge[i].a=read();edge[i].b=read();
	}
	sort(edge+1,edge+m+1);
	for (int i=1;i<=n;i++) FA[i]=po[i]=i;
	for (int i=1;i<=m;i++) {
		addedge(i);
		while (i<m && edge[i].a==edge[i+1].a) addedge(++i);
		if (find(1)==find(n)) {
			split(1,n);
			ans=min(ans,edge[i].a+mx[n]);
		}
	}
	if (ans==1e9) puts("-1");
	else printf("%d",ans);
	return 0;
}

发表于 分类于 ，

原理：
https://wenku.baidu.com/view/75906f160b4e767f5acfcedb
http://www.cnblogs.com/flashhu/p/8324551.html

模板题： https://www.luogu.org/problemnew/show/P3690

0：后接两个整数(x,y)，代表询问从x到y的路径上的点的权值的xor和。保证x到y是联通的。
1：后接两个整数(x,y)，代表连接x到y，若x到y已经联通则无需连接。
2：后接两个整数(x,y)，代表删除边(x,y)，不保证边(x,y)存在。
3：后接两个整数(x,y)，代表将点x上的权值变成y。 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
#include<iostream>
#include<cstdio>
#include<algorithm> //一定要加
using namespace std;
int val[300005],s[300005];
int ch[300005][2],fa[300005];
bool reversed[300005];
int sta[300005],top;
inline int read() {
	char ch=0;int sum=0;
	while (ch>'9'||ch<'0') ch=getchar();
	while (ch>='0'&&ch<='9') sum=sum*10+ch-'0',ch=getchar();
	return sum;
}
inline void reverse(int x) {
	swap(ch[x][0],ch[x][1]);//注意使用algorithm
	reversed[x]^=1;//若有标记，则已经翻转 
}
inline void pushdown(int x) {
	if (reversed[x]) {
		if (ch[x][0]) reverse(ch[x][0]);
		if (ch[x][1]) reverse(ch[x][1]);
		reversed[x]=0;
	}
}
inline void pushup(int x) {
	s[x]=s[ch[x][0]]^s[ch[x][1]]^val[x];
}
inline bool notroot(int x) {
	return (ch[fa[x]][0]==x)||(ch[fa[x]][1]==x);
}
inline void rotate(int x) {
	int fa1=fa[x],fa2=fa[fa1],side=(ch[fa1][1]==x),c=ch[x][side^1];
	fa[x]=fa2;if (notroot(fa1)) ch[fa2][ch[fa2][1]==fa1]=x;//注意区别以及顺序 
	ch[fa1][side]=c;if (c) fa[c]=fa1;
	fa[fa1]=x;ch[x][side^1]=fa1;
	pushup(fa1);pushup(x);
}
inline void splay(int x) {//全部转到根 
	int u=x,top=0;
	while (notroot(u)) sta[++top]=u,u=fa[u];//预先把所有标记下放 
	sta[++top]=u;
	while (top) pushdown(sta[top--]);
	while (notroot(x)) {
		int fa1=fa[x],fa2=fa[fa1];
		if (notroot(fa1)) {//注意区别 
			if ((ch[fa2][0]==fa1)^(ch[fa1][0]==x)) rotate(x);
            else rotate(fa1);
		}
		rotate(x);
	}
}
inline void access(int x) {
	int u=0;
	while (x!=0) {
		splay(x);
		ch[x][1]=u;
		pushup(x);//别忘 
		u=x;
		x=fa[x];
	}
}
inline void makeroot(int x) {
	access(x);splay(x);
	reverse(x);
}
inline int findroot(int x) {
	access(x);splay(x);
	while (ch[x][0]) pushdown(x),x=ch[x][0];
	splay(x);//别忘把根转回来 
	return x;
}
inline void split(int x,int y) {
	makeroot(x);
	access(y);splay(y);
}
inline void link(int x,int y) {
	makeroot(x);
	if (findroot(y)!=x) fa[x]=y;//x在findroot(y)后被转到了根
}
inline void cut(int x,int y) {
	makeroot(x);
	if (findroot(y)==x && fa[y]==x && ch[x][1]==y) {//x在findroot(y)后被转到了根
		fa[y]=ch[x][1]=0;
		pushup(x);
	}
}
int main() {
	int n=read(),m=read();
	for (int i=1;i<=n;i++) val[i]=read();
	while (m--) {
		int op=read(),x=read(),y=read();
		if (op==0) {
			split(x,y);
			printf("%d\n",s[y]);
		}
		else if (op==1) link(x,y);
		else if (op==2) cut(x,y);
		else if (op==3) {splay(x);val[x]=y;pushup(x);}
		
	}
	return 0;
}