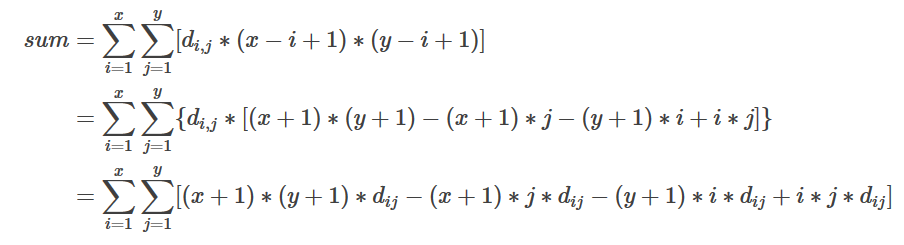基本操作
1
2
3
4
5
6
7
8
9
10
11
12
13
|
struct BIT {
LL c[MAXN];
inline int lowbit(int x) {return x&(-x);}
inline void update(int x,LL val) {
for (;x<=n;x+=lowbit(x)) c[x]+=val;
}
inline LL getsum(int x) {
LL sum=0;
for (;x>0;x-=lowbit(x)) sum+=c[x];
return sum;
}
};
|
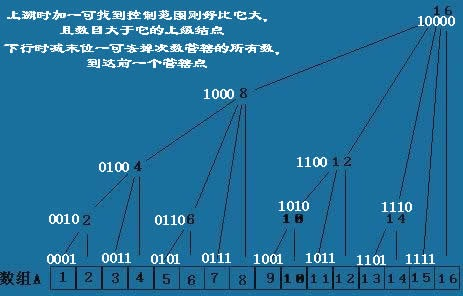
c[i]表示a[i-lowbit(i)+1]~a[i]的和
c[i]维护的点数量为,i在二进制下最后一个1是右数第几位
1.单点修改,区间查询
1
2
3
4
| for (int i=1;i<=n;i++) {
scanf("%d",&a[i]);
update(i,a[i]);
}
|
1
| LL ans=getsum(r)-getsum(l-1);
|
2.区间修改,单点查询
将d[i]+1以后做一遍前缀和,发现区间[i,n]都+1了
于是将区间修改转换为做前缀和的单点修改。
(也可以这么理解,设a[i]的改变值差分后得到d[i],前缀和会把中间项全部消掉,最后只留下这个点的改变值。)
1
2
| update(l,val);
update(r+1,-val);
|
3.区间修改,区间查询
还是那个数组d,d[i]在前缀和意义下是区间[i,n]的共同增量。
查询区间[l,r]的和,就是求sum[r]-sum[l-1],所以现在的问题是求sum[i]。
1
2
3
4
| sum[i]=(a[1]+d[1])+(a[2]+d[1]+d[2])+...+(a[i]+d[1]+d[2]+...+d[i])
=a[1]+a[2]+...+a[i]+d[1]*i+d[2]*(i-1)+d[3]*(i-2)+...+d[i]*1
=sigma(a[x])+sigma(d[x]*(i+1-x))
=sigma(a[x])+(i+1)*sigma(d[x])-sigma(d[x]*x)
|
参考资料
关键代码
d1维护d[x],d2维护d[x]*x,asum是ai前缀和 1
2
3
4
| d1.update(l,val);
d1.update(r+1,-val);
d2.update(l,(LL)val*l);
d2.update(r+1,-(LL)val*(r+1));
|
1
2
3
| LL sum1=asum[l-1]+l*d1.getsum(l-1)-d2.getsum(l-1);
LL sum2=asum[r]+(r+1)*d1.getsum(r)-d2.getsum(r);
printf("%lld\n",sum2-sum1);
|
二维树状数组(未完待续)
此处不妨令左下角为原点(0,0)
1.单点修改,区间求和
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
| struct BIT_2D {
int c[MAXN][MAXM];
inline int lowbit(int x) {return x&(-x);}
inline void update(int xx,int yy,int val) {
for (int x=xx;x<=n;x+=lowbit(x))
for (int y=yy;y<=m;y+=lowbit(y))
c[x][y]+=val;
}
inline LL query(int xx,int yy) {
LL sum=0;
for (int x=xx;x>0;x-=lowbit(x))
for (int y=yy;y>0;y-=lowbit(y))
sum+=c[x][y];
return sum;
}
};
|
设修改点(x,y)
询问左下角(x1,y1)到右上角(x2,y2),满足x1<=x2,y1<=y2
1
| LL ans=getsum(x2,y2)-getsum(x1-1,y2)-getsum(x2,y1-1)+getsum(x1-1,y1-1);
|
2.区间修改,单点求和
3.区间修改,区间求和
对于原矩阵A,用矩阵dij表示(i,j)−(n,m)的增量,那么子矩阵(1,1)−(x,y)的和为:
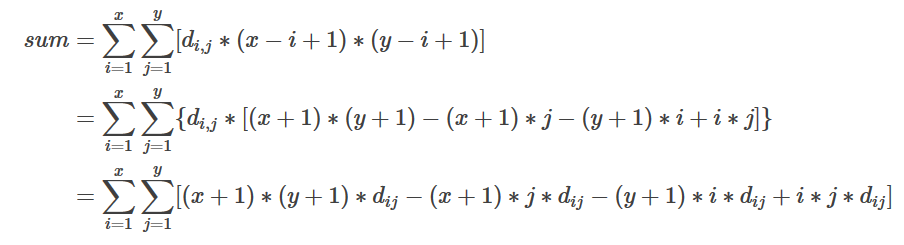
因此,用四个树状数组分别维护:dij,(i∗dij),(j∗dij),(i∗j∗dij)
最后,贴一个二维树状数组的模板。
参考资料1
参考资料2