1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
| #pragma GCC optimize(2)
#include <iostream>
#include <cstdio>
#include <set>
#include <vector>
#include <climits>
#define Pair pair<LL,LL>
#define mp(x,y) make_pair(x,y)
#define fi first
#define se second
using namespace std;
typedef long long LL;
const int MAXN=1e5+5;
const int MAXM=1e6+5;
struct Line {
mutable LL k,b,p;
Line() {}
Line(LL k,LL b,LL p):k(k),b(b),p(p){}
bool operator<(const Line &res) const {return k<res.k;}
} anss[MAXN];
typedef multiset<Line>::iterator mlit;
typedef vector<Pair>::iterator vcit;
struct Data:multiset<Line> {
inline LL fl(LL a,LL b) {
if ((a^b)<0) return a/b-(a%b!=0);
return a/b;
}
inline bool check(iterator x,iterator y) {
if (y==end()) {x->p=INT_MAX;return false;}
if (x->k == y->k) x->p=((x->b > y->b)?INT_MAX:INT_MIN);
else x->p=fl(y->b - x->b, x->k - y->k);
return x->p >= y->p;
}
inline void add(LL k,LL b) {
mlit t=insert(Line(k,b,0)),y=t,x=t;
y++;
while (check(t,y)) erase(y++);
if (t!=begin() && check(--x,t)) erase(t++),check(x,t);
t=x;
while (t!=begin() && (--x)->p >= t->p) erase(t++),check(x,t),t=x;
}
} ans;
int head[MAXN],vet[MAXN*2],nxt[MAXN*2],num;
Pair w[MAXN*2];
int sz[MAXN],mxs[MAXN],rt;
bool vis[MAXN];
int n,m;
inline int read() {
char ch=getchar();int sum=0;
while (ch>'9' || ch<'0') ch=getchar();
while (ch>='0' && ch<='9') sum=sum*10+ch-'0',ch=getchar();
return sum;
}
void print(LL x) {
if (x>9) print(x/10);
putchar(x%10+'0');
}
inline void addedge(int x,int y,int k,int b) {
num++;vet[num]=y;w[num]=mp(k,b);nxt[num]=head[x];head[x]=num;
num++;vet[num]=x;w[num]=mp(k,b);nxt[num]=head[y];head[y]=num;
}
void getroot(int x,int fa,int tot) {
sz[x]=1;mxs[x]=0;
for (int e=head[x];e;e=nxt[e]) {
int v=vet[e];
if (v==fa || vis[v]) continue;
getroot(v,x,tot);
sz[x]+=sz[v];
mxs[x]=max(mxs[x],sz[v]);
}
mxs[x]=max(mxs[x],tot-sz[x]);
if (mxs[x]<mxs[rt]) rt=x;
}
void getpath(int x,int fa,LL k,LL b,Data &a) {
int son=0;
for (int e=head[x];e;e=nxt[e]) {
int v=vet[e];
if (v==fa || vis[v]) continue;
getpath(v,x,k+w[e].fi,b+w[e].se,a);
son++;
}
if (!son) a.add(k,b);
}
inline void update(Data &a,Data &b) {
vector<Pair> vec1,vec2;
for (mlit it=a.begin();it!=a.end();++it) {
if (!vec1.empty() && (it->k)==vec1[vec1.size()-1].fi) {
vec1[vec1.size()-1].se=max(vec1[vec1.size()-1].se,it->b);
}
else vec1.push_back(mp(it->k,it->b));
}
for (mlit it=b.begin();it!=b.end();++it) {
if (!vec2.empty() && (it->k)==vec2[vec2.size()-1].fi) {
vec2[vec2.size()-1].se=max(vec2[vec2.size()-1].se,it->b);
}
else vec2.push_back(mp(it->k,it->b));
}
LL s1=0,s2=0;
while (s1<vec1.size() && s2<vec2.size()) {
ans.add(vec1[s1].fi+vec2[s2].fi,vec1[s1].se+vec2[s2].se);
if (s1+1==vec1.size()) s2++;
else if (s2+1==vec2.size()) s1++;
else {
double x1=-(vec1[s1+1].se-vec1[s1].se)/(double)(vec1[s1+1].fi-vec1[s1].fi);
double x2=-(vec2[s2+1].se-vec2[s2].se)/(double)(vec2[s2+1].fi-vec2[s2].fi);
if (x1<x2) s1++;
else s2++;
}
}
}
Data merge(int l,int r,vector<Data> &q) {
if (l==r) {
Data tt;
tt.add(0,0);
update(tt,q[0]);
return q[l];
}
int mid=(l+r)>>1;
Data t1=merge(l,mid,q),t2=merge(mid+1,r,q);
if (t1.size()>t2.size()) swap(t1,t2);
update(t1,t2);
for (mlit it=t1.begin();it!=t1.end();++it) t2.add(it->k,it->b);
return t2;
}
void solve(int x,int tot) {
vis[x]=1;
vector<Data> vec;
Data blank;blank.add(0,0);
for (int e=head[x];e;e=nxt[e]) {
int v=vet[e];
if (vis[v]) continue;
vec.push_back(blank);
getpath(v,x,w[e].fi,w[e].se,vec[vec.size()-1]);
}
if (!vec.empty()) merge(0,vec.size()-1,vec);
for (int e=head[x];e;e=nxt[e]) {
int v=vet[e];
if (vis[v]) continue;
rt=0;
int tt=sz[v];
if (tt>sz[x]) tt=tot-sz[x];
getroot(v,x,tt);
solve(rt,tt);
}
}
int main() {
n=read(),m=read();
ans.add(0,0);
for (int i=1;i<n;i++) {
int x=read(),y=read(),k=read(),b=read();
addedge(x,y,k,b);
}
mxs[0]=(n<<1);rt=0;
getroot(1,0,n);
solve(rt,n);
int top=0;
for (mlit it=ans.begin();it!=ans.end();++it) anss[++top]=(*it);
for (LL i=0,j=1;i<m;i++) {
while (anss[j].p<i) j++;
print(anss[j].k*i+anss[j].b);putchar(' ');
}
return 0;
}
|
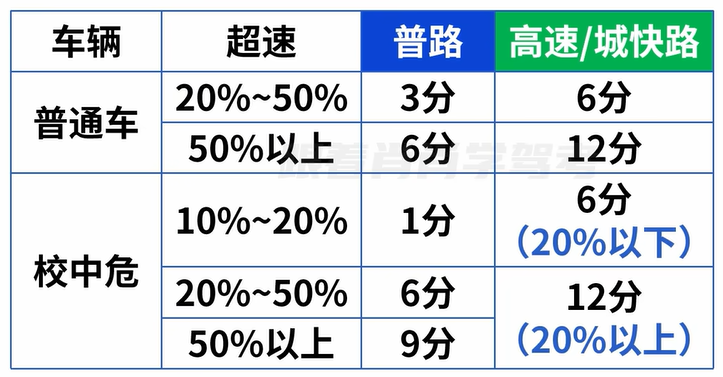3 6 6 12
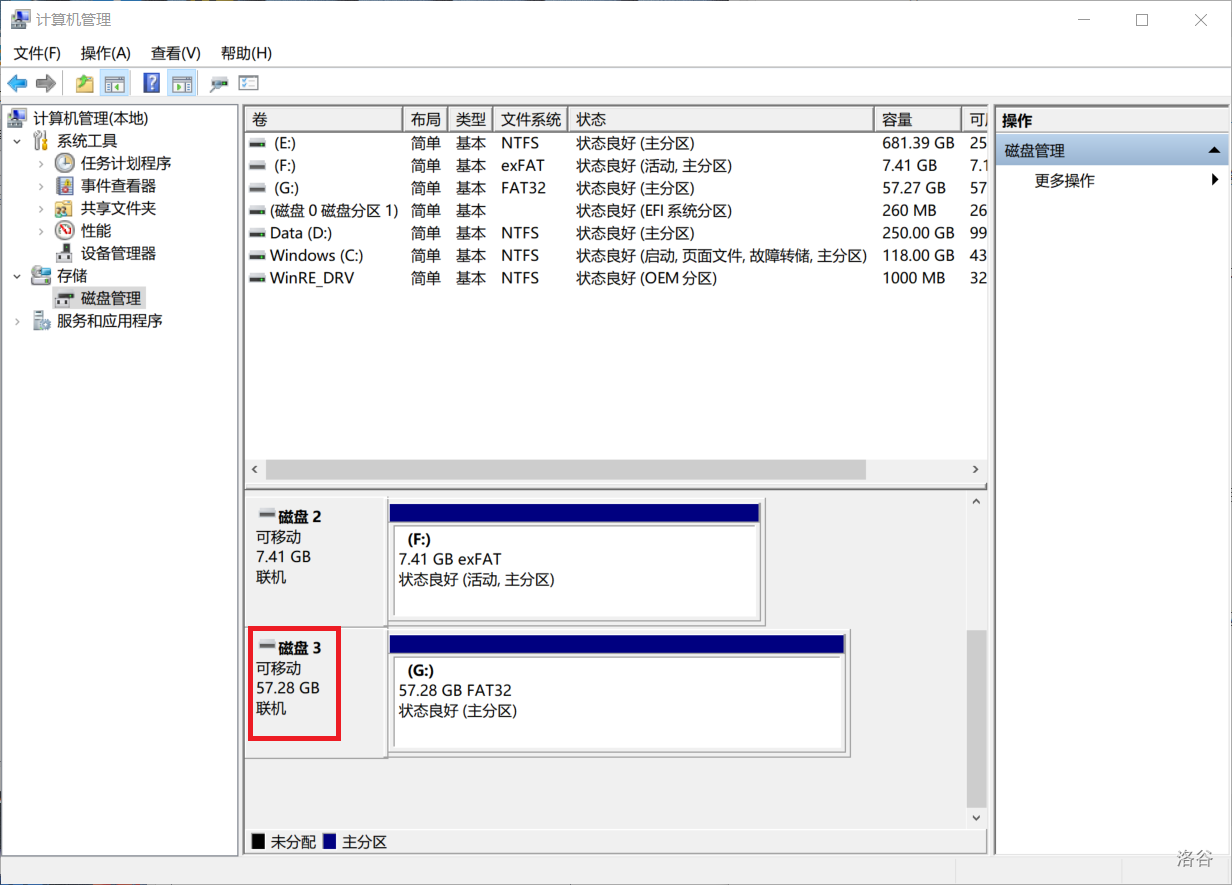记住自己的U盘的磁盘编号（比如我这里是磁盘3）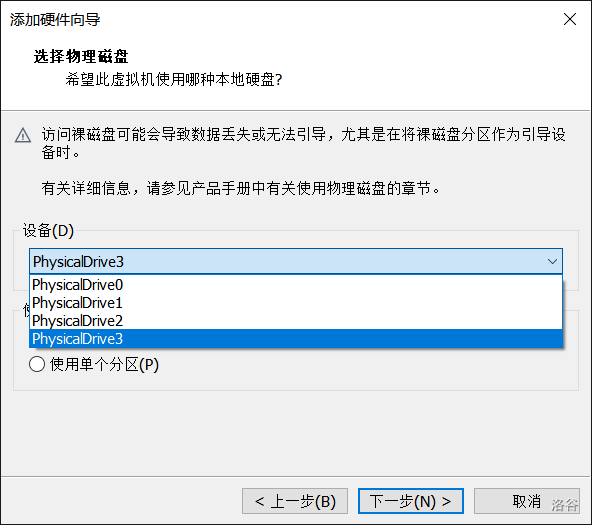
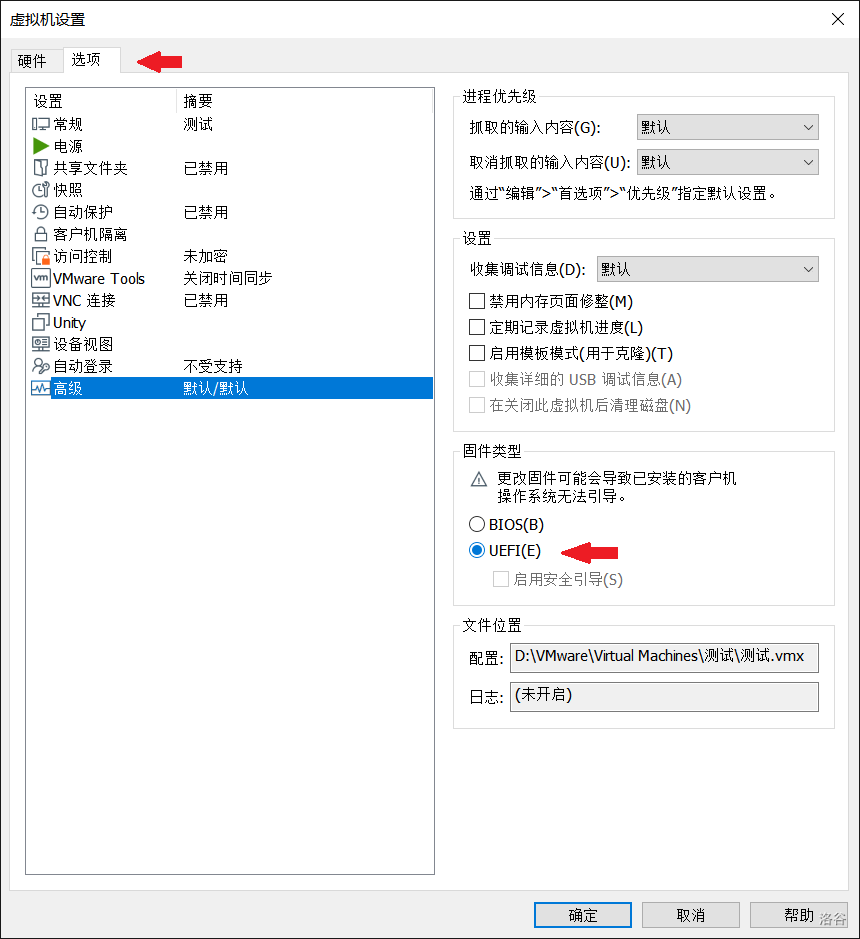
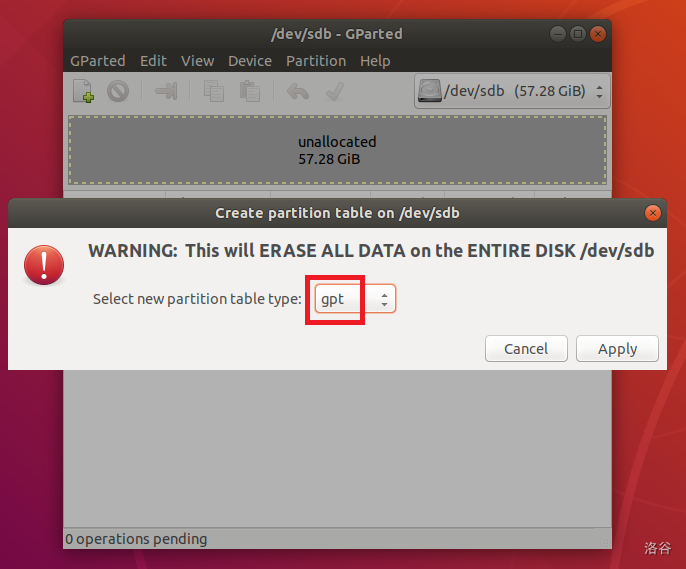
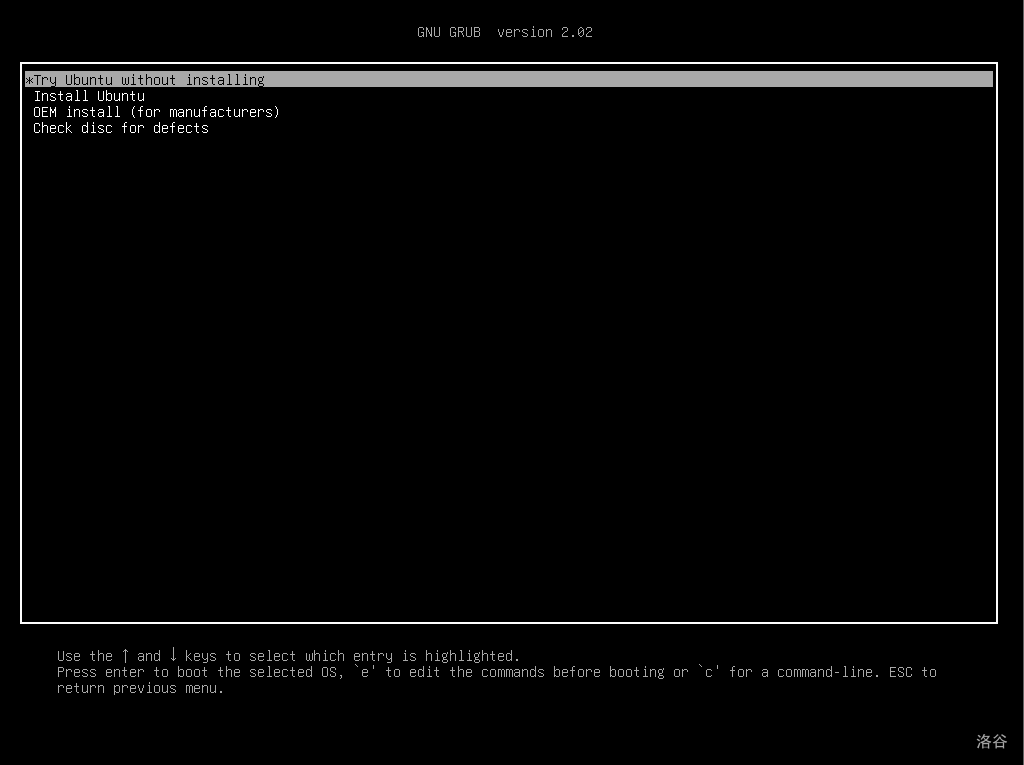选择"Try Ubuntu without installing"。开机后启动 Gparted。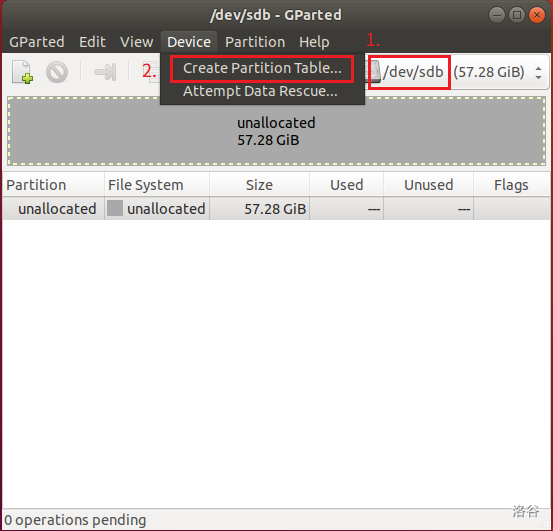
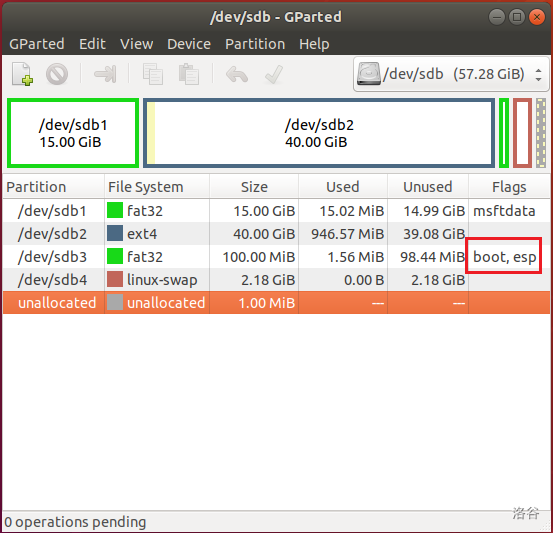
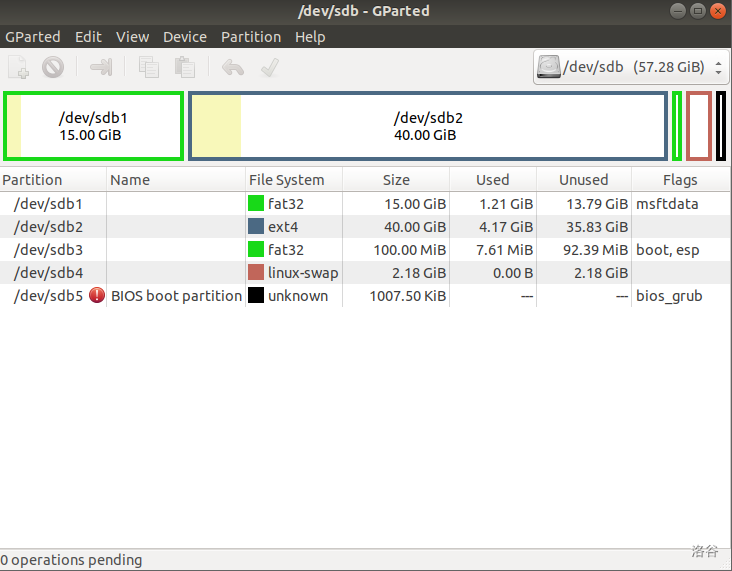
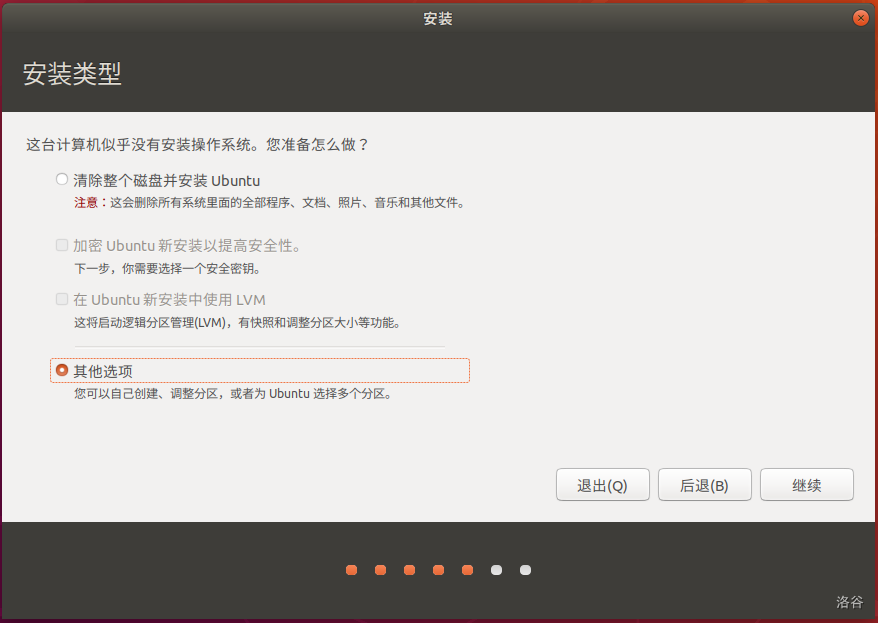
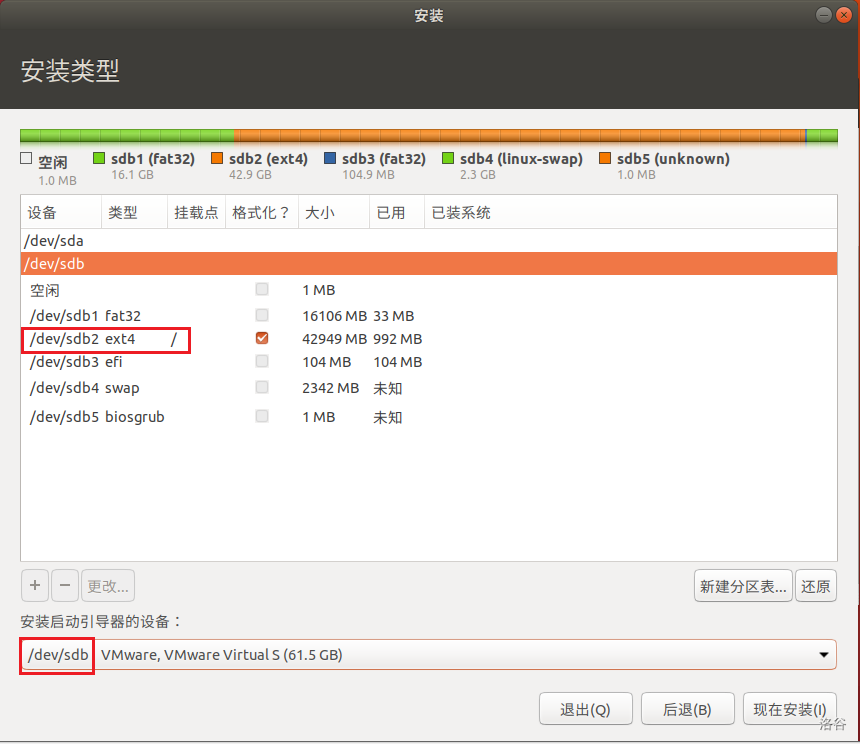把 ext4 挂载到 /。也可以按照自己的需要来设置。
选择 Try Ubuntu。
